본 강의에서의 학습목표는 다음과 같다.
- The problem of the Linear classifier
- What is a Convolution layer - convolution, stride, padding
- What is a Pooling layer - why do we need pooling?, max pooling, average pooling
Recall: One Problem of the Linear Classifier
- A linear classifier creates a straight decision boundary between the classes
- When the data points are not linearly separable, a linear classifier cannot perfectly divide the classes
Recall: How a Neural Network handle this problem?
By combining multiple layers, NN finds the function which maps input data into this higher-dimensional space where the data can be separated using a linear classifier!
hidden layer들만 쌓으면 linear layer이므로 activation function을 추가하여 non-linearity를 들어가게 한다.
Another Problem of the Linear Classifier

- Linear classifier doesn't respect the spatial structure of images!
- We need to define new computational nodes that operate on images!
How a Neural Network handle this problem?

Convolution
이미지에 각 픽셀마다의 값들이 있으면 filter(학습가능한 가중치들)가 이미지와 계산을 거친 후 bias를 더하여 하나의 output 값이 나오며 아래 그림과 같이 작동한다.



Convolution in 3D

5x5x3 filter를 통해 다음과 같은 결과를 얻을 수 있다.

N개의 filter를 사용하면 N차원의 activation map이 생성된다.

32 x 32 x 3 image를 5 x 5 x 3 filter를 사용하면 왜 28 x 28 x 1의 결과가 나오는지에 알아보자.
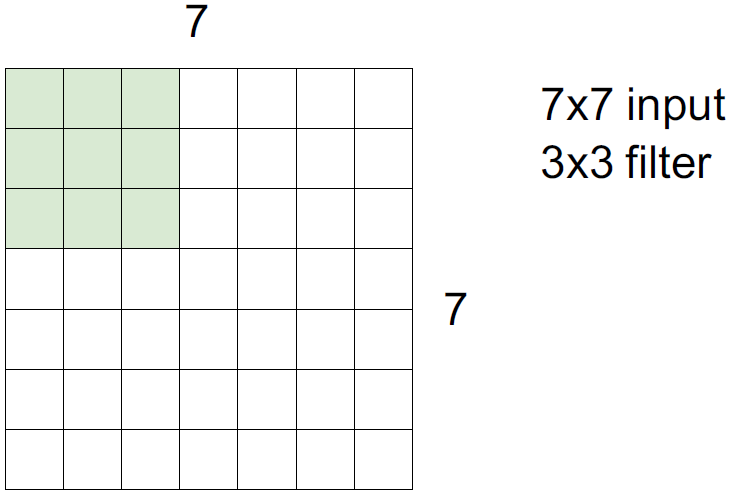

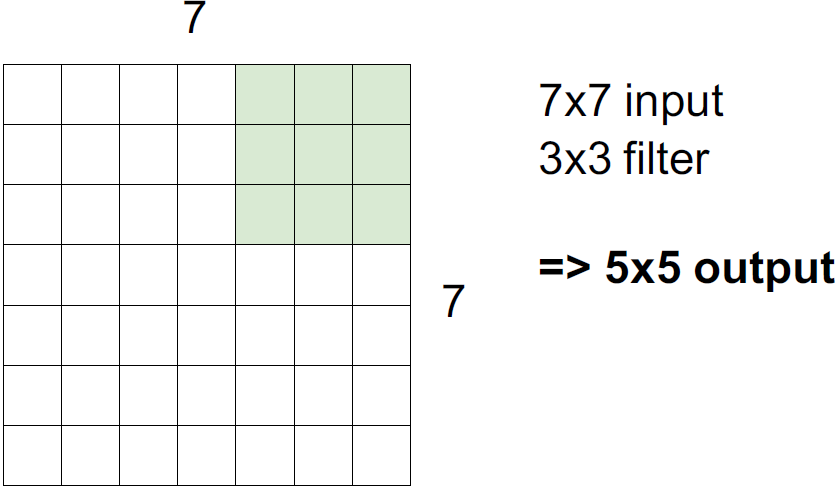
만약 stride = 2 이면, 2칸씩 건너띄면서 계산하기 때문에 3 x 3의 결과로 나온다.
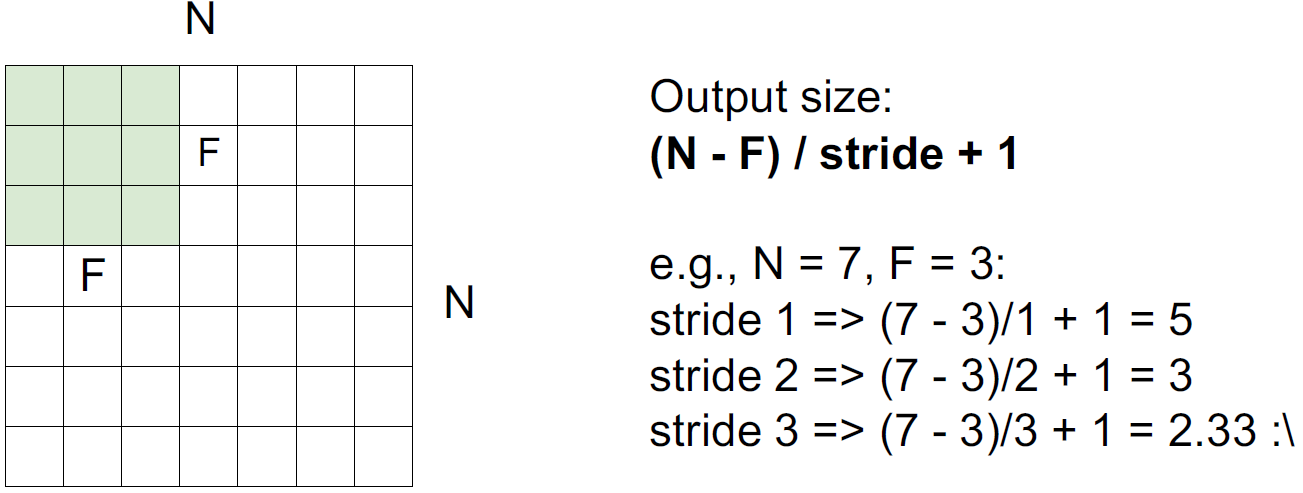
만약 stride = 3 이면, 칸이 맞지가 않으므로 적용할 수 없다.
image 크기와 filter 크기, stride를 알면 output size를 알 수 있고 공식화하면 다음과 같다.
padding이란 무엇일까?
이미지의 가장자리에 0으로 채워주는 것을 zero padding이라 한다.
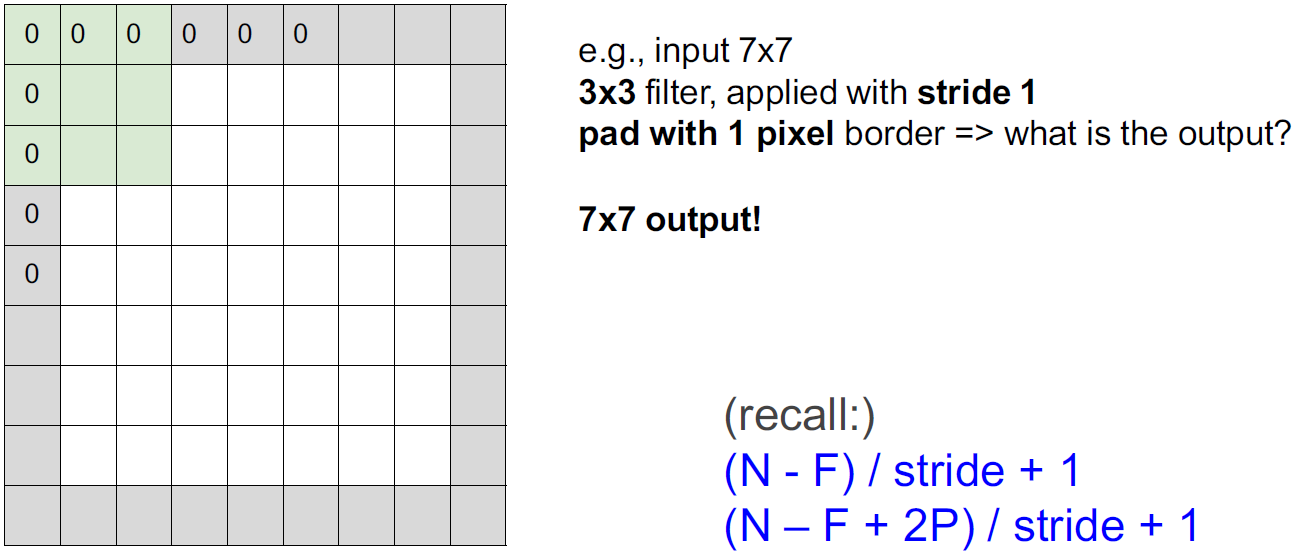
zero padding을 하는 이유는 output 형태를 그대로 유지하기 위해서이다.
stride = 1이라 가정하면 zero-padding with (F-1)/2일때, input size를 보존할 수 있다.
1 x 1 Convolution Layer
This is useful when reducing the channel dimension (without losing the spatial dimensions H, W)
1 x 1 filter를 가지고 실제로 많이 사용한다. spatial dimension은 유지하면서 파라미터도 덜 쓰면서 channel dimension을 늘리고 줄이고 할 때 사용한다.
Example: A Convolution Layer
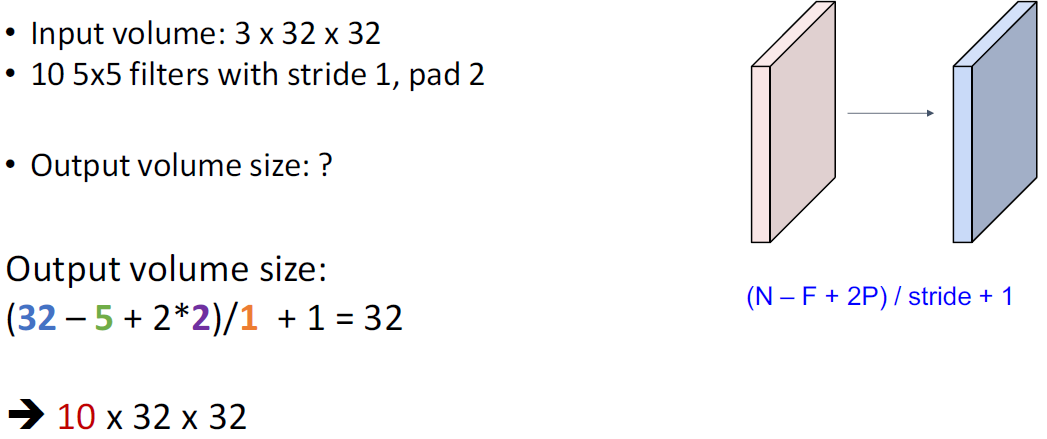

계산량 = filter size * output size (bias 무시한다고 가정)

linear layer처럼 convolution layer도 여러 개 쌓아서 사용할 수 있다. 더 많은 hidden layer가 있을수록 더 복잡한 차원의 boundary를 학습할 수 있다. 하지만, convolution 역시 activation function이 들어가야한다. convolution은 덧셈과 곱셈으로밖에 이루어져있기 때문에 convolution 역시 linear하다. 따라서, activation function이 중간중간 들어가야한다.
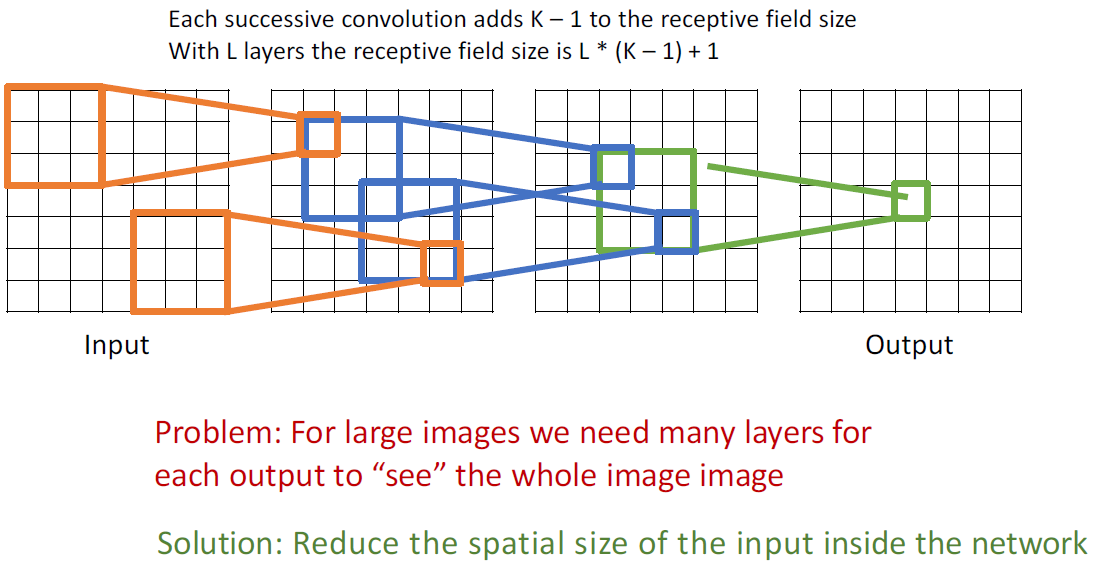
Receptive Fields
image size가 1024 x 1024 혹은 그 이상일때, output 결과에서의 한 점이 이 모든 정보를 포함하려면 커널 사이즈를 키우던지 layer를 많이 쌓아야하는데 그렇게 되면 파라미터와 계산량이 증가한다. 이를 해결하기 위해, input의 spatial size를 줄임으로써 receptive field를 높여준다. 그 중 하나의 방법이 아까 배운 stride를 사용하는 방법이 있으며 이를 down-sampling이라한다.
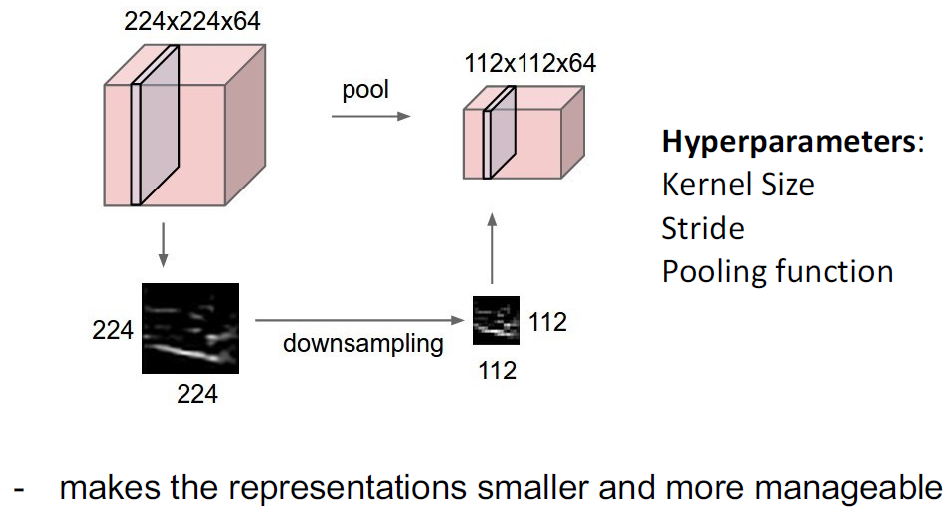
Pooling Layers: Another way to downsample
representation을 더 작게 만들고 감당가능하게 만들어주기 위해 pooling layer를 사용한다. 이를 위해, kernel size, stride, pooling function이 등장한다.
Max POOLING

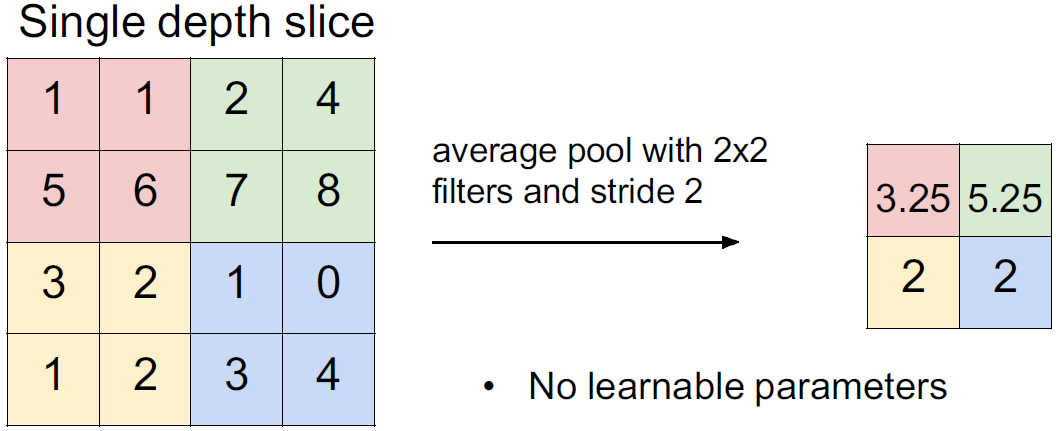
Average POOLING
'Lectures > 딥러닝영상인식1' 카테고리의 다른 글
| [Lecture 6] Convolutional Neural Network & Training Neural Network (0) | 2024.12.16 |
|---|---|
| [Lecture 5] Convolutional Neural Network (CNN) (1) | 2024.10.21 |
| [Lecture 3] Backpropagation (2) | 2024.10.20 |
| [Lecture 2] Neural Network and Loss Function (0) | 2024.09.24 |
| [Lecture 1] Image Classification and Classifiers (0) | 2024.09.06 |



