이번 강의에서의 학습목표는 다음과 같다.
- What is Backpropagation Algorithm?
- Backpropagation with Linear Classifier
- Backpropagation with Neural Network
- Backpropagation with Vector/Matrix
Back-propagation은 1986년에 "Learning Representations by Back-Propagating Errors" 논문에서 소개된 방법이다. 보통 2012년에 딥러닝이 시작되었다하고 2016~2017년에 활발히 연구가 시작되었다.
Image Classification에서는 Input과 weight가 곱해져서 output 값을 만든다. 그 후, 실제 값과 output 값의 차이를 loss function을 통해 Error 값을 계산한다. Error를 계산하기 위해 forward 방향으로 계산을 하고 Error를 정보를 바탕으로 backward 방향으로 weight들을 업데이트한다. "back"은 뒤로, "propagation"은 전파의 의미로 backward 방향으로 전파를 해서 뭔가를 하는 것이 backpropagation이라고 생각하면 된다. backpropagation의 자세한 내용은 이제부터 차근차근 알아간다.
Backpropagation with Linear Classifier
Single layer network가 있다고 하면 각 데이터들은 weight와 곱해져서 output을 출력한다. output 값과 실제 값을 다양한 loss function을 이용해서 오차 값을 계산한다. loss function은 저번 강의에서 배운 hinge loss, cross-entropy loss 등등 있다. loss 값을 계산한 후, backpropagation을 하는데 가중치별로 미분하는 것이다. w1이 변할 때, loss가 얼마나 변하는지 계산하는 것이다. 미분한 값을 기존 w1값에서 뺀다. w1(new) = w1(old) - (loss를 w1으로 미분한 값). 가중치 값들을 이용해서 loss값을 계산하는데 우리가 원하는 것은 loss 값이 낮아지는 가중치 값들을 찾는 것이 중요하다. 즉, loss가 작아지는 방향으로 가중치들을 업데이트 하는 것이 backpropation의 핵심이다. loss가 작아지는 방향으로 각 가중치들을 업데이트 하면 loss가 낮아지는 것이고 이는 우리가 학습시키고 있는 모델의 eroor 값이 낮아지는 것으로 좋게 흘러가기 때문에 이를 학습. 즉, Learning이라 한다.
Backpropagation with Neural Network
Multi-layer network에서 backpropagation을 사용할 때, chain rule이라는 것을 사용한다.
간단한 예시로 알아보자.
f = wx + b가 있다고 하자. (f: output, w: weight, x: input, b: bias) 이를 neural network 형태로 시각화하면 다음과 같다.

위 그림처럼 input 값들이 있으면 f 값이 -14가 나온다. 다양한 loss function들이 있지만 여기서는 loss 값이 f값(-14)와 같다고 가정하자. input 값은 그냥 데이터이므로 관심 대상이 아니고 w와 b값을 업데이트를 해야하므로 loss를 w와 b로 미분한 값을 계산한다.
b에 따라 loss가 어떻게 변하는지 계산하고 w에 따라 loss가 어떻게 변하는지 계산한다. loss를 b로 미분한 값은 바로 계산을 못하므로 chain rule을 이용해서 loss를 f로 미분한 값과 f를 b로 미분한 값을 곱하여 계산한다. loss를 f에 대해 미분한 값은 1이다(동일하다고 가정했으므로). f를 b로 미분한 값은 f = q + b를 b로 미분한 것이므로 1이다. 즉, loss를 b로 미분한 값은 1이다. loss를 w로 미분한 값은 방금과 같은 방식으로 동일하게 하면 -2가 나온다.
미분한 값을 기존 값에서 빼서 새로운 가중치 값으로 업데이트한다. b(new) = b(old) - loss/b = -4 - 1 = -5, w(new) = 7이다. 새롭게 업데이트한 가중치로 loss를 계산해보면 q = -14, f = -19이다. f=loss랑 같다고 가정했으니 loss는 더 낮아져 좋아진 것을 알 수 있다.
Patterns in Gradient Flow
각 연산마다의 패턴들이 있다. add gate에서 z = x + y 와 같이 예시를 들어 계산해보면 아래와 같이 미분값들을 계산할 때 패턴을 가지는 것을 알 수 있다. (외울 필요는 없다)

Backpropagation을 좀 더 복잡한 식의 예제로 알아보자. 여기서도 loss = f 값이라고 가정하자.

loss를 1/x로 미분한 값을 계산하면 다음과 같다.

그 다음 미분한 값들을 계산하면 다음과 같다.


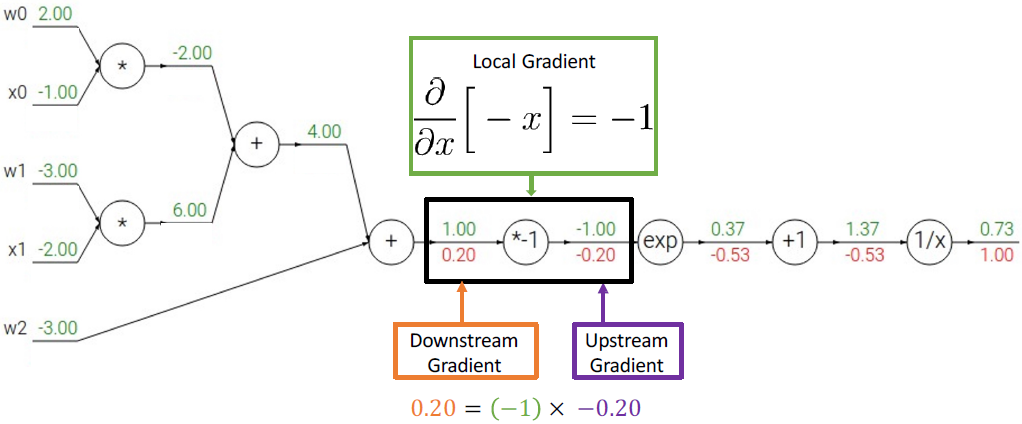
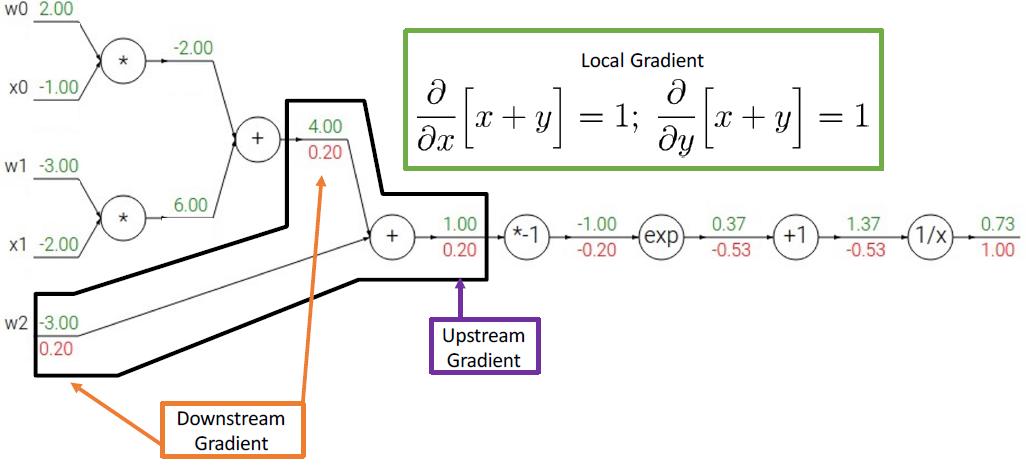
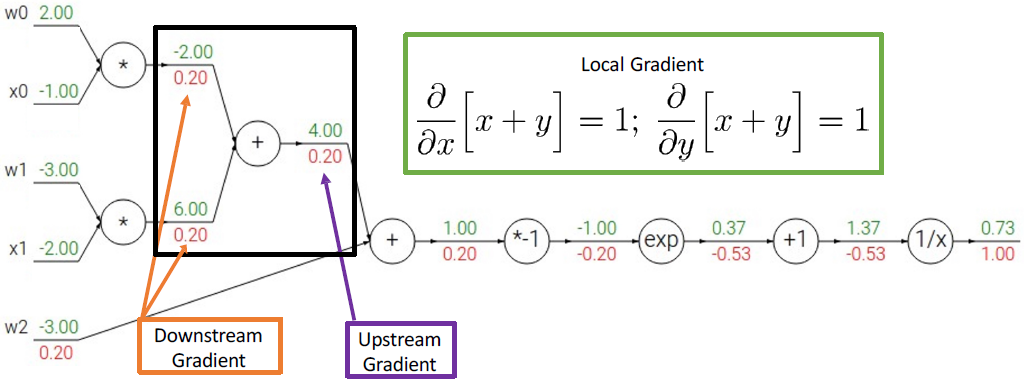
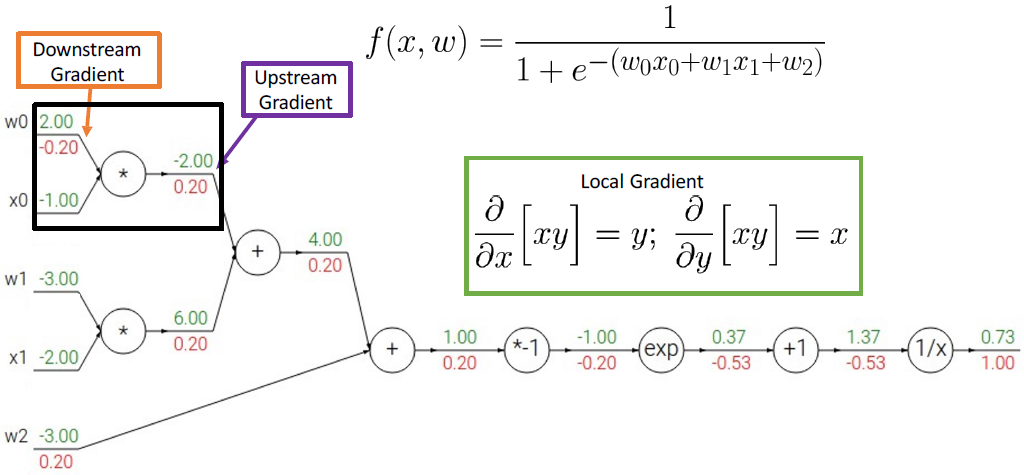
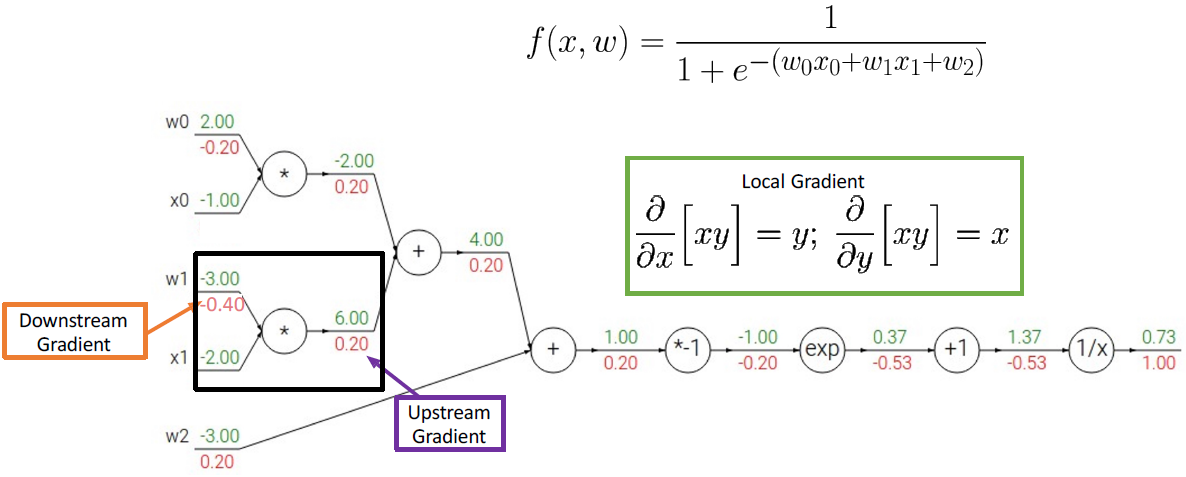
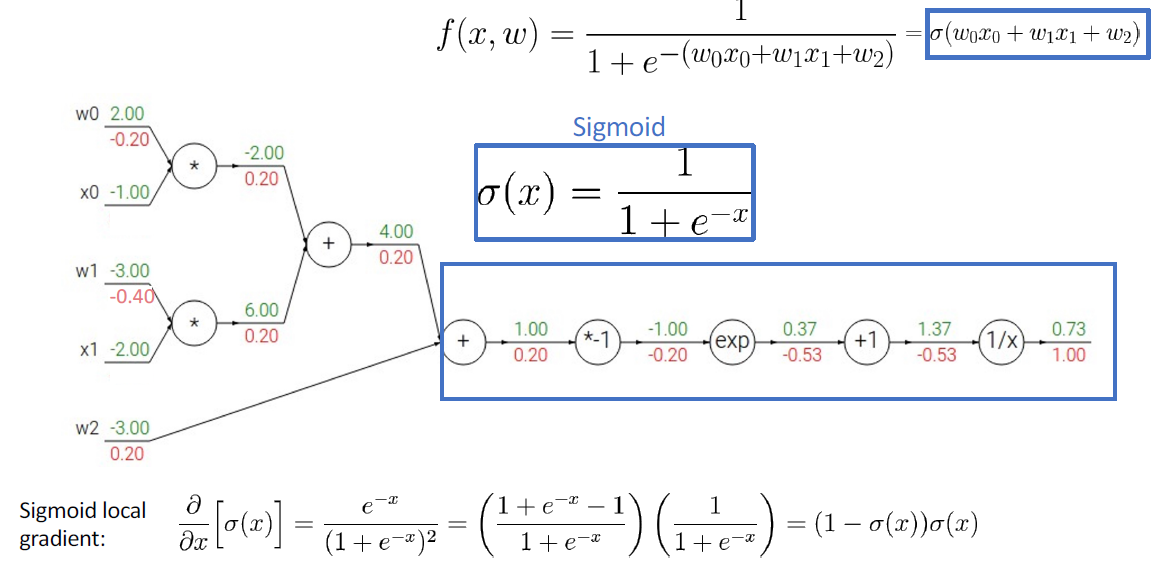
그런데 이 식은 activation function 중에 하나인 sigmoid 식이다. sigmoid를 미분해서 최종 미분 값과 같은지도 한 번 보면 다음과 같다.
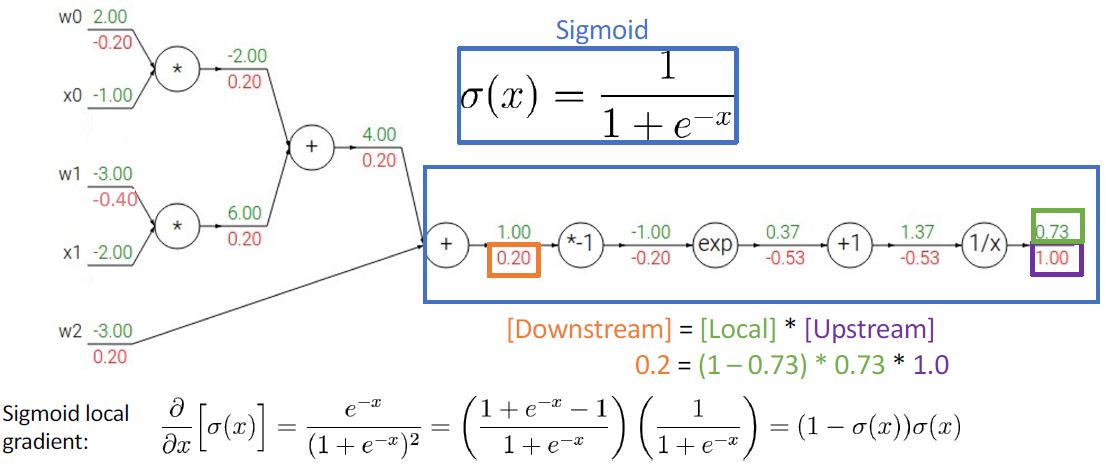
Backpropagation with Vector/Matrix
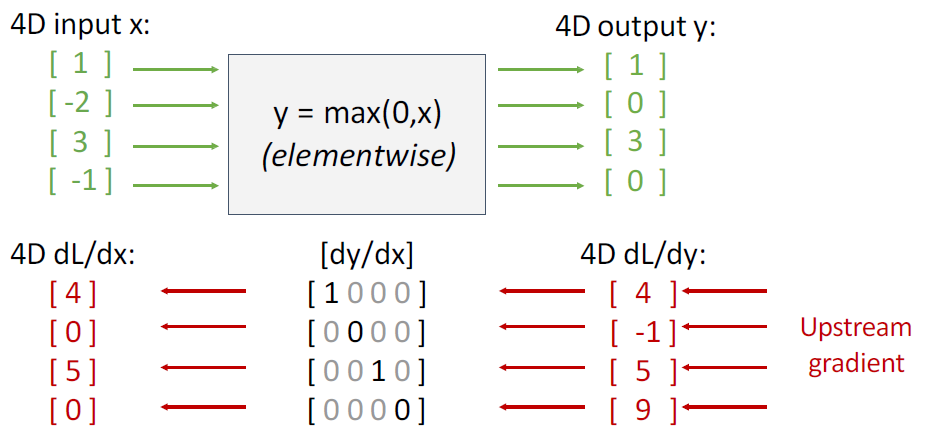
지금까지의 backpropagation을 scalar 값으로 계산하였다. x, y를 각각 N차원, M차원의 벡터라고 했을 때, y를 x로 미분한 것은 N x M 형태의 행렬을 가진다.
간단한 neural network 형태로 예시를 보면 다음과 같다.
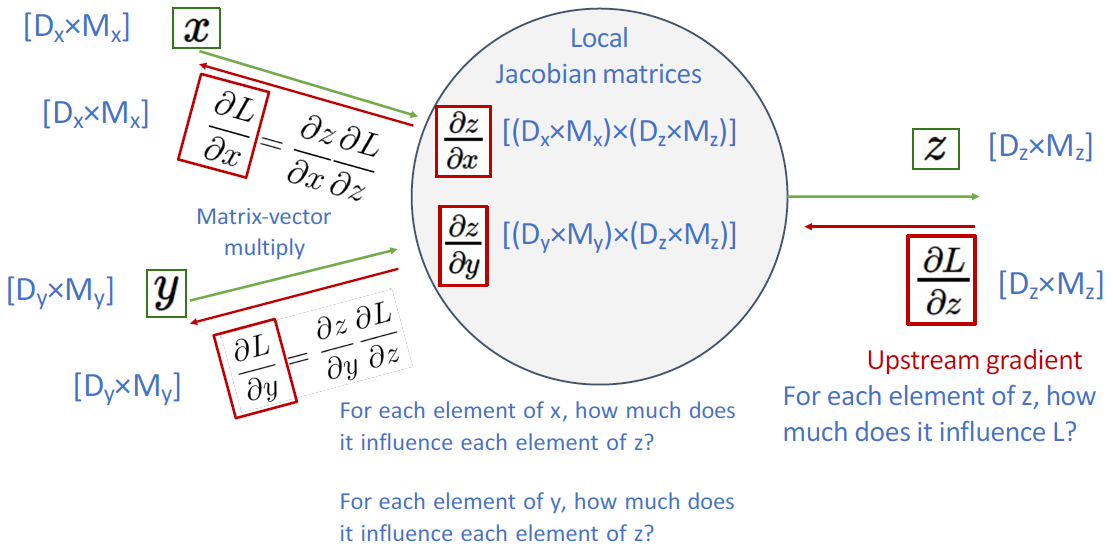
y = max(0,x)에서의 미분값을 행렬로 나타내면 다음과 같다.
'Lectures > 딥러닝영상인식1' 카테고리의 다른 글
| [Lecture 6] Convolutional Neural Network & Training Neural Network (0) | 2024.12.16 |
|---|---|
| [Lecture 5] Convolutional Neural Network (CNN) (1) | 2024.10.21 |
| [Lecture 4] Convolution (3) | 2024.10.21 |
| [Lecture 2] Neural Network and Loss Function (0) | 2024.09.24 |
| [Lecture 1] Image Classification and Classifiers (0) | 2024.09.06 |



