혹시 잘못된 부분이나 수정할 부분이 있다면 댓글로 알려주시면 감사하겠습니다.
Loss Function은 머신러닝, 딥러닝에서 필수적인 부분이고 논문에서도 자주 나오는 용어로 대표적인 것들만 정리하고자 한다.
Loss Function이란 무엇일까?
Loss Function(손실 함수)는 하나의 input data에서 나온 오차(예측값과 실제값의 차이)를 계산하는 함수이다.
즉, Loss Function의 값을 최소화되도록 가중치(weight)와 편향(bias)를 찾는 것이 목표
* Cost Function(비용 함수) : 모든 input dataset에서 나온 오차를 계산하는 함수
* Object Function(목적 함수) : 어떤 값을 최대화 혹은 최소화 시키기 위해 정의되는 함수
Loss Function < Cost Function < Object Function 순으로 포괄적인 개념이라 생각해도 괜찮을 듯하다.
Loss Function은 데이터의 형태에 따라 정의할 수 있다.
데이터의 형태는 크게 수치형 데이터와 범주형 데이터로 나눌 수 있다.
수치형 데이터는 회귀 모델을 사용하고 범주형 데이터는 분류 모델을 사용한다.
회귀 모델에 대한 Loss Function
1. MAE(Mean Absolute Error)
MAE(Mean Absolute Error; 평균절대오차)는 출력값과 실제값 차이에 대한 평균

2. MSE(Mean Squared Error)
MSE(Mean Square Error; 평균제곱오차)는 출력값과 실제값 차이의 제곱에 대한 평균
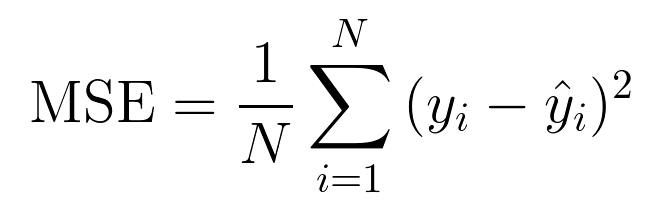
3. RMSE(Root Mean Squared Error)
RMSE(Root Mean Squared Error; 평균제곱근오차)는 MSE에 루트를 씌워준 것
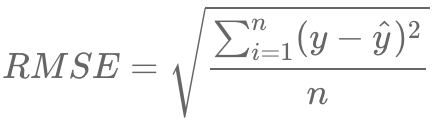
분류 모델에 대한 Loss Function
1. Cross Entropy
Cross Entropy(교차 엔트로피)를 알아보기 전에 Entropy를 먼저 알아보고자 한다.
어떤 특정 현상이 발생할 확률을 p라고 할 때, Entropy의 공식은 다음과 같다.
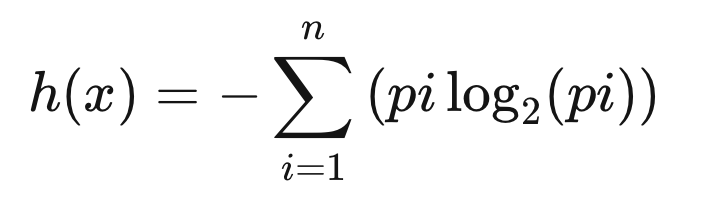
특정 사건이 발생활 확률 p에 로그를 취해준 p를 곱한 후 모두 더한 값에 -를 취해준다.
p의 확률이 모호할수록(50%에 가까울수록) Entropy 값은 커지고 p의 확률이 확실할수록(100% 혹은 0%에 가까울수록) Entropy 값은 작아진다.
Cross Entropy는 Entropy와 유사한 개념으로 Entropy는 정답이 나올 확률만을 대상으로 측정한 값이었다면 Cross Entropy는 모델에서 예측한 확률과 실제 정답확률을 모두 사용해 측정한 값이다. 즉, 모델에서 예측한 확률값이 실제값과 비교했을 때 틀릴 수 있는 정보량을 의미한다. Entropy와 마찬가지로 그 값이 적을수록 모델이 데이터를 더 잘 예측하는 모델임을 의미한다.
모델에서 각 클래스에 대해 예측한 확률값을 q, 실제 값의 확률을 p, 클래수 개수를 n이라고 하면 공식은 다음과 같다.
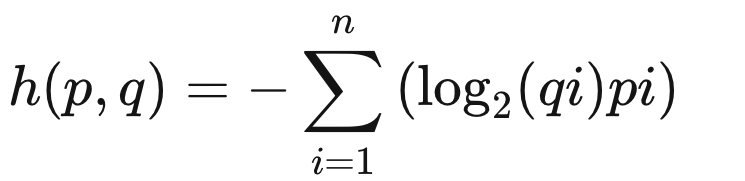
Cross Entropy는 Entropy와 다르게 로그를 취해준 값이 실제 정답 확률이 아닌 모델에서 예측한 확률 값이다.
ex) 세 가지 색깔(빨간색, 파랑색, 초록색)의 공에서 빨간 공을 뽑아야 할 때, Cross Entropy를 계산해보자. ['빨간색', '파랑색', '초록색'] 순서를 가질 때, p=[1, 0, 0]이 된다.
- q=[0.33, 0.33, 0.33]일 경우, Cross Entropy = -1*log0.33 - 0*log0.33 - 0*log0.33 = 1.599
- q=[0.7, 0.2, 0.1]일 경우, Cross Entropy = -1*log0.7 - 0*log0.2 - 0*log0.1 = 0.514
- q=[1, 0, 0]일 경우, Cross Entropy = -1*log1 - 0*log0 - 0*log0 = 0
2. KL Divergence (Kullback-Leibler Divergence)
KL Divergence는 두 확률분포 간의 정보량의 차이를 측정하는 데 사용되는 개념이다. 수식은 다음과 같다.
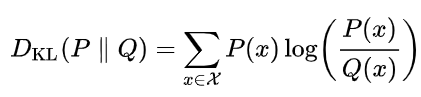
KL Divergence의 의미를 좀 더 직관적으로 이해하기 위해 식을 다음과 같이 변형해보자.

마지막 줄을 보면 두 분포의 Cross Entropy에서 Entropy를 뺀 값이 된다. 즉 KL Divergence는 두 확률분포의 차이를 보여주는 척도이지만 Cross Entropy에서 기준분포 P(x)의 Entropy를 빼줌으로써 (두 분포 사이의 차이에서 기준 분포 자체의 불확실성을 제거함으로써) 두 분포가 얼마나 서로 다른 정보를 가지고 있는지를 순수하게 측정하는 방법이다.
KL Divergence 예제를 한 번 보자.

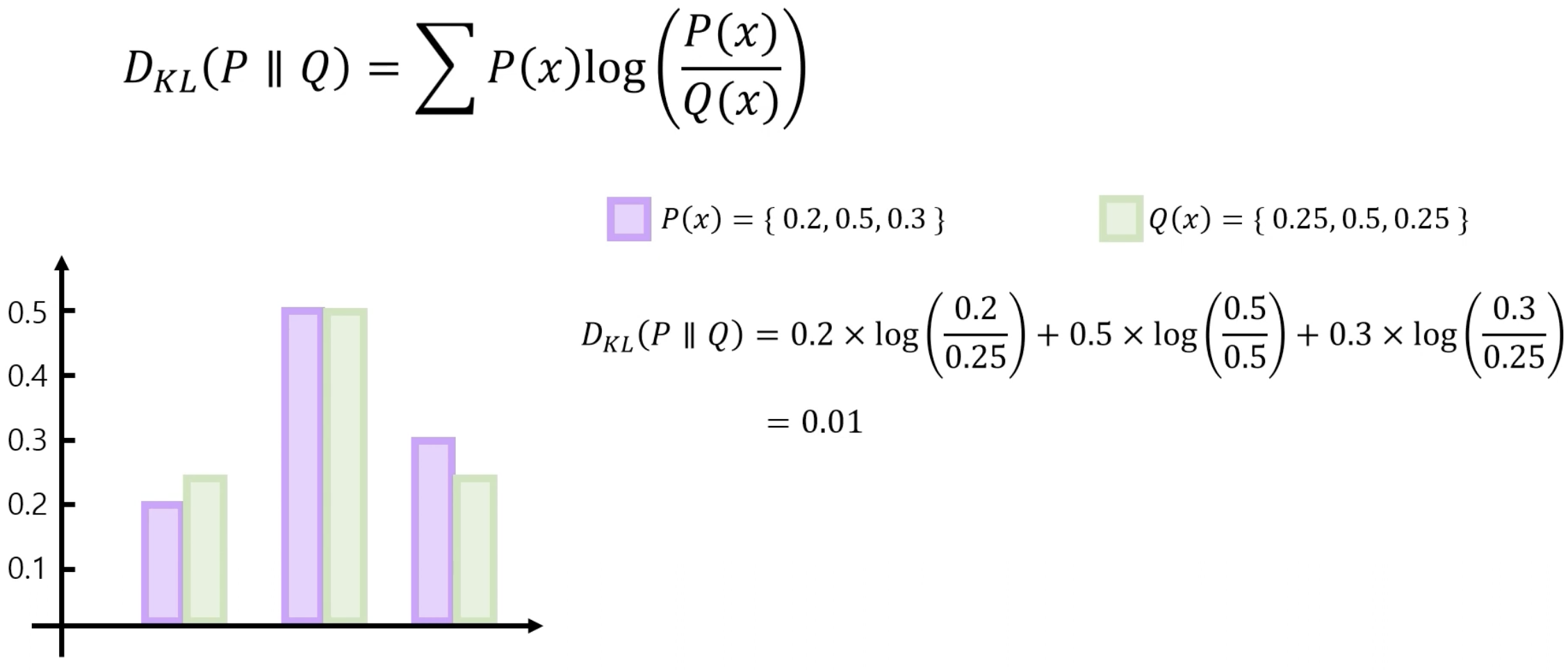
첫 번째 예제와 두 번째 예제 KL Divergence는 각각 0.0305, 0.01이다. 두 분포가 비슷할수록 KL Divergence 값이 줄어든다. 이와 같이 두 분포가 유사하면 KL Divergence의 값은 0에 수렴하게 된다. 또한, KL Divergence는 비대칭이다. 기준 분포가 P에서 Q로 바뀌면 같은 분포여도 KL Divergence 값은 다르다. 이는 특정 분포를 기준 분포로 하여 상대적인 차이를 계산하기 때문에 이런 특징을 보인다.
KL Divergence는 두 분포의 차이를 계산할 때, 기준 분포를 고려해야하고 0부터 무한까지의 값이 나올 수 있어 모델을 업데이트 할 때 문제가 발생할 수 있다. 이러한 문제점을 보완하기 위해 Jensen-SHannon Divergence가 있다.
Conclusion
Loss Function(손실 함수) : 하나의 input data에서 나온 오차(예측값과 실제값의 차이)를 계산하는 함수
회귀 모델에 대한 Loss Function
1. MAE : 출력값과 실제값 차이에 대한 평균

2. MSE : 출력값과 실제값 차이의 제곱에 대한 평균
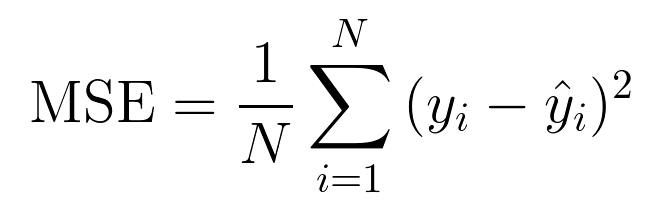
3. RMSE : MSE에 루트를 씌어준 것
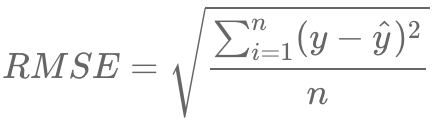
분류 모델에 대한 Loss Function
1. Cross Entropy : 모델에서 예측한 확률과 실제 정답확률을 비교했을 때 틀릴 수 있는 정보량
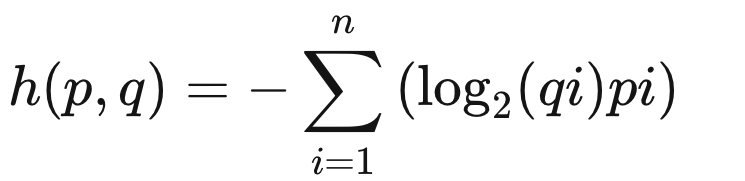
2. KL Divergence : 두 확률분포 간의 정보량의 차이를 측정하는 데 사용되는 개념 (Cross Entropy - Entropy)
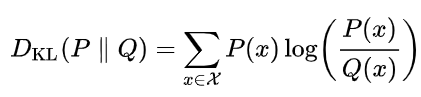
'Deep Learning Study > Mathematics' 카테고리의 다른 글
| [미적분학] L1, L2 Regularization (0) | 2024.04.21 |
|---|---|
| [미적분학] 테일러 급수 (2) | 2024.04.09 |
| [미적분학] Back Propagation (0) | 2024.03.02 |
| [미적분학] Optimization(GD, SGD) (0) | 2024.02.29 |
| [확률 및 통계학] Likelihood (0) | 2024.02.27 |



